maxdrawdown
Compute maximum drawdown for one or more price series
Description
MaxDD = maxdrawdown(Data)N-vector
MaxDD and identifies start and end indexes of maximum
drawdown periods for each series in a 2-by-N
matrix MaxDDIndex.
[
adds an optional output for MaxDD,MaxDDIndex] = maxdrawdown(___)MaxDDIndex.
Examples
Calculate Maximum Drawdown
Calculate the maximum drawdown (MaxDD) using example data with a fund, market, and cash series:
load FundMarketCash
MaxDD = maxdrawdown(TestData)MaxDD = 1×3
0.1658 0.3381 0
The maximum drop in the given time period was 16.58% for the fund series, and 33.81% for the market series. There was no decline in the cash series, as expected, because the cash account never loses value.
maxdrawdown also returns the indices (MaxDDIndex) of the maximum drawdown intervals for each series in an optional output argument.
[MaxDD, MaxDDIndex] = maxdrawdown(TestData)
MaxDD = 1×3
0.1658 0.3381 0
MaxDDIndex = 2×3
2 2 NaN
18 18 NaN
The first two series experience their maximum drawdowns from the second to the 18th month in the data. The indices for the third series are NaNs because it never has a drawdown.
The 16.58% value loss from month 2 to month 18 for the fund series is verified using the reported indices.
Start = MaxDDIndex(1,:); End = MaxDDIndex(2,:); (TestData(Start(1),1) - TestData(End(1),1))/TestData(Start(1),1)
ans = 0.1658
ans = 0.1658
Although the maximum drawdown is measured in terms of returns, maxdrawdown can measure the drawdown in terms of absolute drop in value, or in terms of log-returns. To contrast these alternatives more clearly, you can work with the fund series, assuming an initial investment of 50 dollars:
Fund50 = 50*TestData(:,1); plot(Fund50); title('\bfFive-Year Fund Performance, Initial Investment 50 usd'); xlabel('Months'); ylabel('Value of Investment');
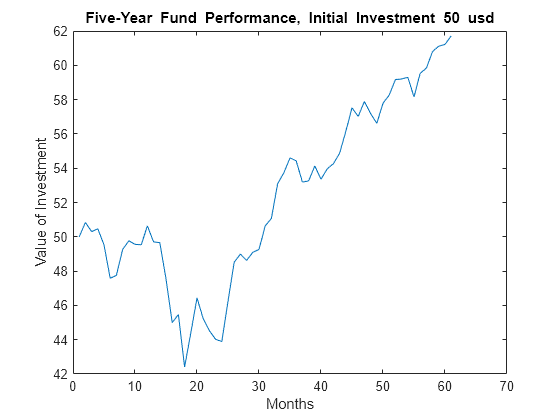
First, compute the standard maximum drawdown, which coincides with the results above because returns are independent of the initial amounts invested.
MaxDD50Ret = maxdrawdown(Fund50)
MaxDD50Ret = 0.1658
Next, compute the maximum drop in value, using the 'arithmetic' argument.
[MaxDD50Arith, Ind50Arith] = maxdrawdown(Fund50,'arithmetic')MaxDD50Arith = 8.4285
Ind50Arith = 2×1
2
18
The value of this investment was $50.84 in month 2, but by month 18 the value was down to $42.41, a drop of $8.43. This is the largest loss in dollar value from a previous high in the given time period. In this case, the maximum drawdown period, from the 2nd to 18th month, is the same independently of whether drawdown is measured as return or as dollar value loss.
[MaxDD50LogRet, Ind50LogRet] = maxdrawdown(Fund50,'geometric')MaxDD50LogRet = 0.1813
Ind50LogRet = 2×1
2
18
Note, the last measure is equivalent to finding the arithmetic maximum drawdown for the log of the series.
MaxDD50LogRet2 = maxdrawdown(log(Fund50),'arithmetic')MaxDD50LogRet2 = 0.1813
Input Arguments
Data — Total return price series
matrix
Total return price series, specified as a
T-by-N matrix with
T samples of N total return price
series.
Data Types: double
Format — (Optional) Format of Data
character vector with value of 'return', 'arithmetic', or 'geometric'
Format of Data, specified as character vector with
the following possible values:
'return'(default) — Maximum drawdown in terms of maximum percentage drop from a peak.'arithmetic'— Maximum drawdown of an arithmetic Brownian motion with drift (differences of data from peak to trough) using the equation
'geometric'— Maximum drawdown of a geometric Brownian motion with drift (differences of log of data from peak to trough) using the equation
Data Types: char
Output Arguments
MaxDD — Maximum drawdown
vector
Maximum drawdown, returned as a
1-by-N vector with maximum
drawdown for each of N time series.
Note
Drawdown is the percentage drop in total returns from the start to the end of a period. If the total equity time series is increasing over an entire period, drawdown is 0. Otherwise, it is a positive number. Maximum drawdown is an ex-ante proxy for downside risk that computes the largest drawdown over all intervals of time that can be formed within a specified interval of time.
Maximum drawdown is sensitive to quantization error.
MaxDDIndex — Start and end indexes for each maximum drawdown period for each total equity time series
vector
Start and end indexes for each maximum drawdown period for each total
equity time series, returned as a
2-by-N vector of start and end
indexes. The first row of the vector contains the start indexes and the
second row contains the end indexes of each maximum drawdown period.
References
[1] Christian S. Pederson and Ted Rudholm-Alfvin. "Selecting a Risk-Adjusted Shareholder Performance Measure." Journal of Asset Management. Vol. 4, No. 3, 2003, pp. 152–172.
Version History
Introduced in R2006b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other bat365 country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)
Asia Pacific
- Australia (English)
- India (English)
- New Zealand (English)
- 中国
- 日本Japanese (日本語)
- 한국Korean (한국어)