Main Content

Conduct Cointegration Test Using Econometric Modeler

This example models the annual Canadian inflation and interest rate series by using the Econometric Modeler app. The example performs the following actions in the app:

  1. Test each raw series for stationarity.

  2. Test for cointegration using the Engle-Granger cointegration test.

  3. Test for cointegration among all possible cointegration ranks using the Johansen cointegration test.

The data set, which is stored in Data_Canada, contains annual Canadian inflation and interest rates from 1954 through 1994.

Load and Import Data into Econometric Modeler

At the command line, load the Data_Canada.mat data set.

load Data_Canada

At the command line, open the Econometric Modeler app.

econometricModeler

Alternatively, open the app from the apps gallery (see Econometric Modeler).

Import DataTimeTable into the app:

  1. On the Econometric Modeler tab, in the Import section, click the Import button .

  2. In the Import Data dialog box, in the Import? column, select the check box for the DataTimeTable variable.

  3. Click Import.

The Canadian interest and inflation rate variables appear in the Time Series pane, and a time series plot of all the series appears in the Time Series Plot(INF_C) figure window.

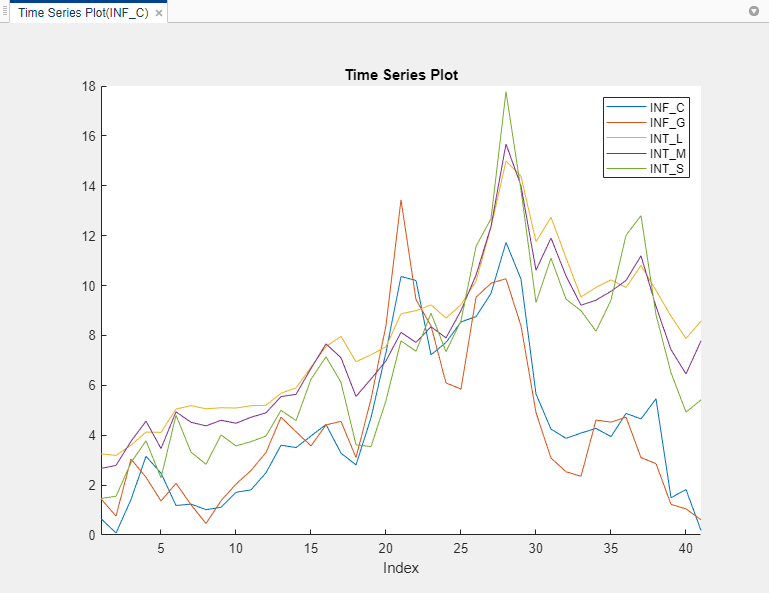
Time series plot of all the series

Plot only the three interest rate series INT_L, INT_M, and INT_S together. In the Time Series pane, click INT_L and Ctrl click INT_M and INT_S. Then, on the Plots tab, in the Plots section, click Time Series. The time series plot appears in the Time Series(INT_L) document.

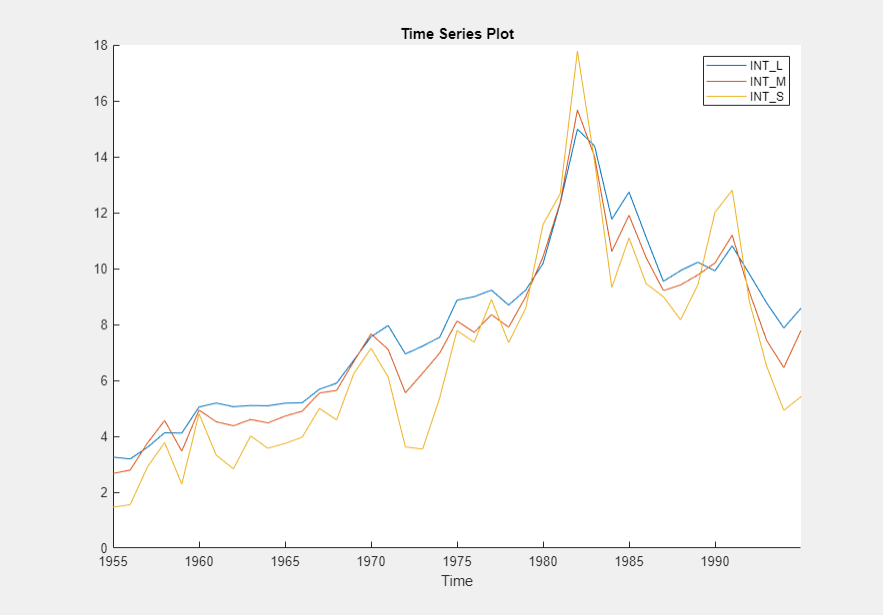
Time series plot of the interest rate series

The interest rate series each appear nonstationary, and they appear to move together with mean-reverting spread. In other words, they exhibit cointegration. To establish these properties, this example conducts statistical tests.

Conduct Stationarity Test

Assess whether each interest rate series is stationary by conducting Phillips-Perron unit-root tests. For each series, assume a stationary AR(1) process with drift for the alternative hypothesis. You can confirm this property by viewing the autocorrelation and partial autocorrelation function plots.

Close all plots in the right pane, and perform the following procedure for each series INT_L, INT_M, and INT_S.

  1. In the Time Series pane, click a series.

  2. On the Econometric Modeler tab, in the Tests section, click New Test > Phillips-Perron Test.

  3. On the PP tab, in the Parameters section, in the Number of Lags box, type 1, and in the Model list select Autoregressive with Drift.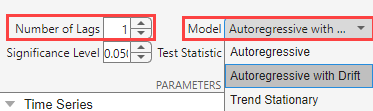

    Phillips-Perron test parameter settings

  4. In the Tests section, click Run Test. Test results for the selected series appear in the PP(series) tab.

Position the test results to view them simultaneously.

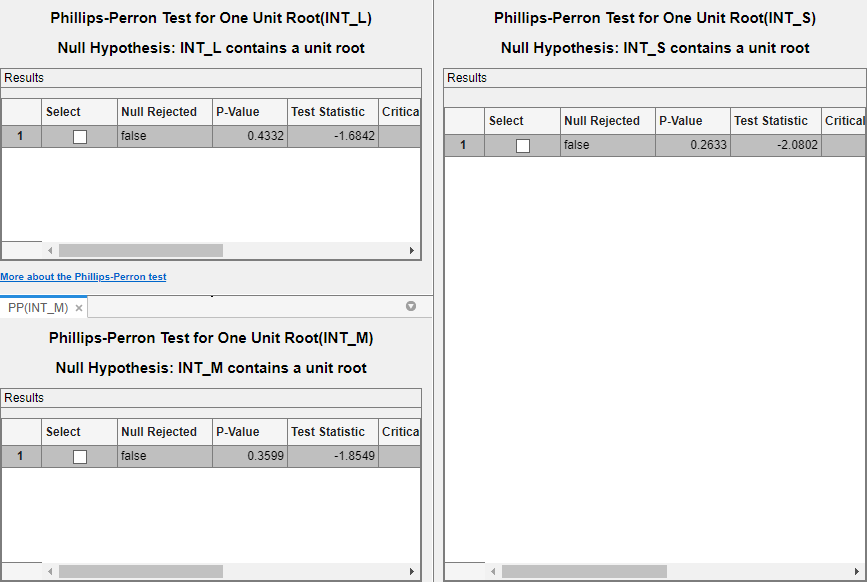
Phillips_perron test results

All tests fail to reject the null hypothesis that the series contains a unit root process.

Conduct Cointegration Tests

Econometric Modeler supports the Engle-Granger and Johansen cointegration tests. Before conducting a cointegration, determine whether there is visual evidence of cointegration by regressing each interest rate on the other interest rates.

  1. In the cointegrating relation, assign INT_L as the dependent variable and INT_M and INT_S as the independent variables. In the Time Series pane, click INT_L.

  2. On the Econometric Modeler tab, in the Models section, click the arrow > MLR.

  3. In the MLR Model Parameters dialog box, select the Include? check boxes of the time series INT_M and INT_S.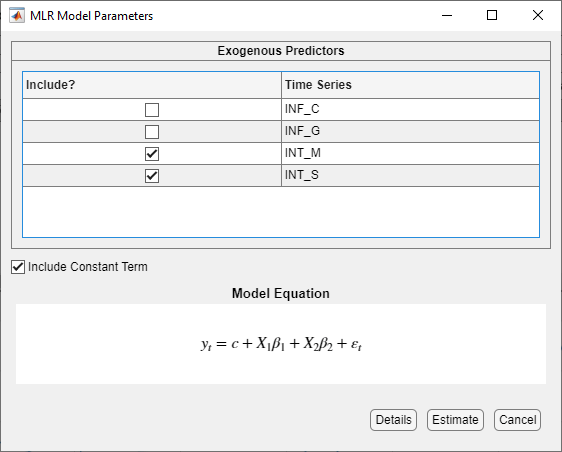

    Multiple linear regression predictor selection

  4. Click Estimate. The model variable MLR_INT_L appears in the Models pane, its value appears in the Preview pane, and its estimation summary appears in the Model Summary(MLR_INT_L) document.

  5. Iterate steps 1 through 4 twice. For the first iteration, assign INT_M as the dependent variable and INT_L and INT_S as the independent variables. For the second iteration, assign INT_S as the dependent variable and INT_M and INT_L as the independent variables.

  6. On each Model Summary(MLR_seriesName) tab, determine whether the residual plot appears stationary.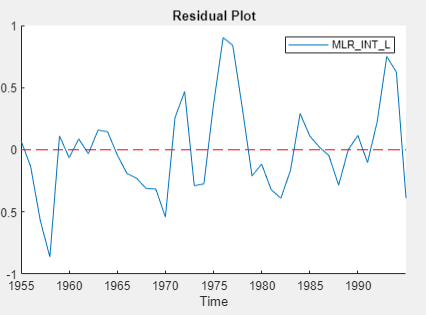

    INT_L residual plot

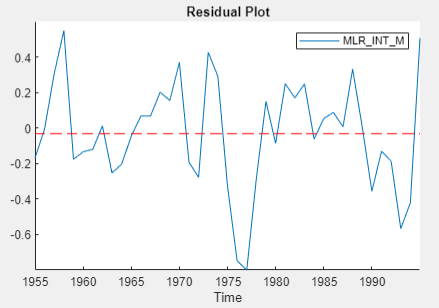
    INT_M residual plot

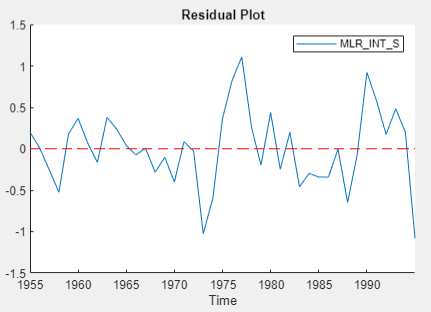
    INT_S residual plot

The residual series of the regression on INT_L appears trending, and the other residual series appear stationary. For the Engle-Granger test, choose INT_S as the dependent variable.

Conduct Engle-Granger Test

The Engle-Granger tests for one cointegrating relation by performing two univariate regressions: the cointegrating regression and the subsequent residual regression (for more details, see Identifying Single Cointegrating Relations). Therefore, to perform the cointegrating regression, the test requires:

  • The response series that takes the role of the dependent variable in the first regression.

  • Deterministic terms to include in the cointegrating regression.

Then, the test assesses whether the residuals resulting from the cointegrating regression are a unit root process. Available tests are the Augmented Dickey-Fuller (adftest) or Phillips-Perron (pptest) test. Both perform a residual regression to form the test statistic. Therefore, the test also requires:

  • The unit root test to conduct, either the adftest or pptest function. The residual regression model for both tests is an AR model without deterministic terms. For more flexible models, such as AR models with drift, call the functions at the command line.

  • Number of lagged residuals to include in the AR model.

Conduct the Engle-Granger test.

  1. In the Time Series pane, click INT_L and Ctrl+click INT_M and INT_S.

  2. In the Tests section, click New Test > Engle-Granger Test.

  3. On the EGCI tab, in the Parameters section:

    1. In the Dependent Variable list, select INT_S.

    2. In the Residual Regression Form list, select PP for the Phillips-Perron unit root test.

    3. In the Number of Lags box, type 1.

      Engle-Granger test parameter settings

  4. In the Tests section, click Run Test. Test results appear in the EGCI document.

  5. In the Tests section, click Run Test again. Test results and a plot of the cointegration relation for the largest rank appear in the EGCI tab.

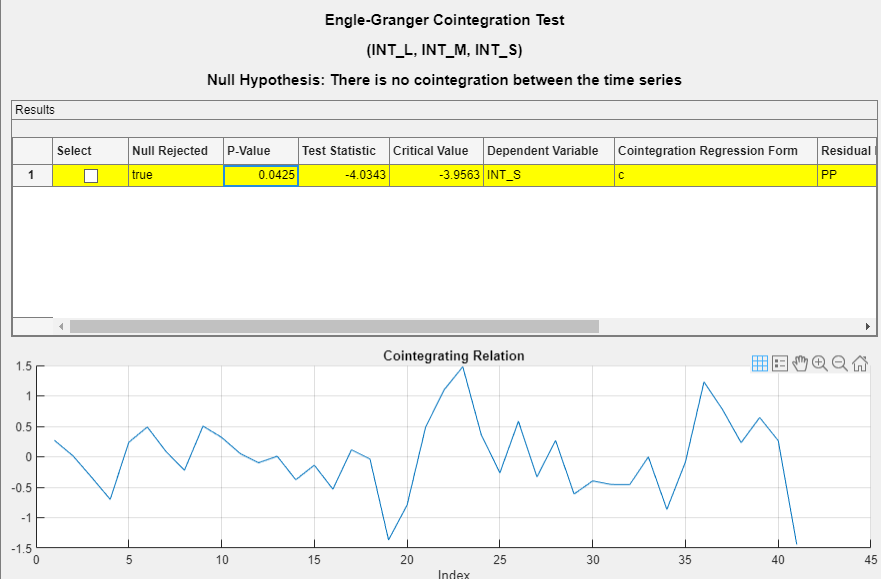
Engle-Granger test results

The test rejects the null hypothesis that the series does not exhibit cointegration. Although the test is suited to determine whether series are cointegrated, the results are limited to that. For example, the test does not give insight into the cointegrating rank, which is required to form a VEC model of the series. For more details, see Identifying Single Cointegrating Relations.

Johansen Test

The Johansen cointegration test runs a separate test for each possible cointegration rank 0 through m – 1, where m is the number of series. This characteristic makes the Johansen test better suited than the Engle-Granger test to determine the cointegrating rank for a VEC model of the series. Also, the Johansen test framework is multivariate, and, therefore, results are not relative to an arbitrary choice for a univariate regression response variable. For more details, see Identifying Multiple Cointegrating Relations.

The Johansen test requires:

  • Deterministic terms to include in the cointegrating relation and the model in levels.

  • Number of short-run lags in the VEC model of the series.

Because the raw series do not contain a linear trend, assume that the only deterministic term in the model is an intercept in the cointegrating relation (H1* Johansen form), and include 1 lagged difference term in the model.

  1. With INT_L, INT_M, and INT_S selected in the Time Series pane, click Tests section, click New Test > Johansen Test.

  2. On the JCI tab, in the Parameters section, in the Number of Lags box, type 1, and in the Model list select H1*.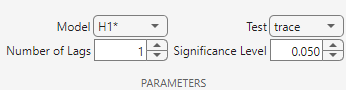

    Johansen test parameter settings

  3. In the Tests section, click Run Test. Test results and a plot of the cointegration relation for the largest rank appear in the JCI tab.

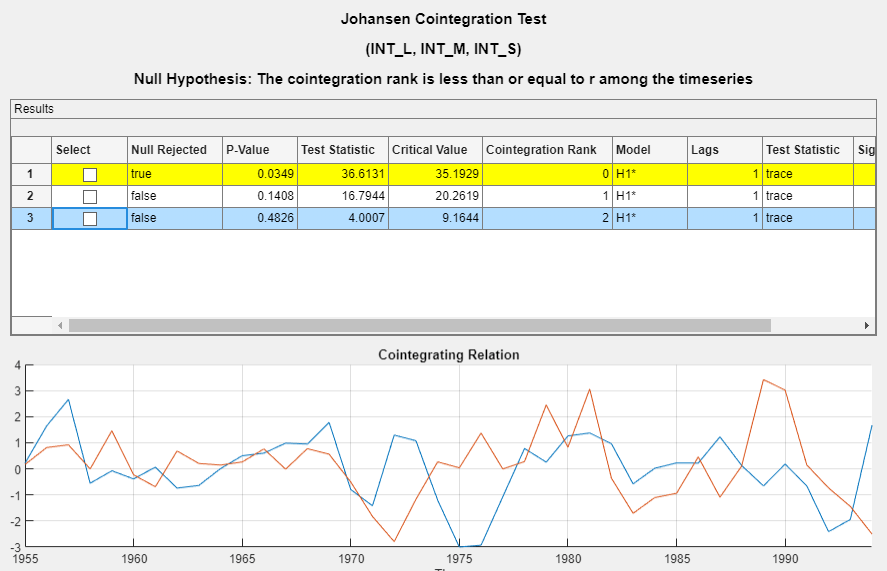
Johansen test results

Econometric Modeler conducts a separate test for each cointegration rank 0 through 2 (the number of series – 1). The test rejects the null hypothesis of no cointegration (Cointegration rank = 0), but fails to reject the null hypotheses of Cointegration rank ≤ 1 and Cointegration rank ≤ 2. The results suggest that the cointegration rank is 1.

See Also

Apps

Objects

Functions

Related Topics