Main Content

Evaluate Surface Fit

Open Live Script

This example shows how to work with a surface fit.

Load Data and Fit a Polynomial Surface

load franke;
surffit = fit([x,y],z,'poly23','normalize','on')
     Linear model Poly23:
     surffit(x,y) = p00 + p10*x + p01*y + p20*x^2 + p11*x*y + p02*y^2 + p21*x^2*y 
                    + p12*x*y^2 + p03*y^3
       where x is normalized by mean 1982 and std 868.6
       and where y is normalized by mean 0.4972 and std 0.2897
     Coefficients (with 95% confidence bounds):
       p00 =      0.4253  (0.3928, 0.4578)
       p10 =      -0.106  (-0.1322, -0.07974)
       p01 =     -0.4299  (-0.4775, -0.3822)
       p20 =     0.02104  (0.001457, 0.04062)
       p11 =     0.07153  (0.05409, 0.08898)
       p02 =    -0.03084  (-0.05039, -0.01129)
       p21 =     0.02091  (0.001372, 0.04044)
       p12 =     -0.0321  (-0.05164, -0.01255)
       p03 =      0.1216  (0.09929, 0.1439)

The output displays the fitted model equation, the fitted coefficients, and the confidence bounds for the fitted coefficients.

Plot the Fit, Data, Residuals, and Prediction Bounds

plot(surffit,[x,y],z)

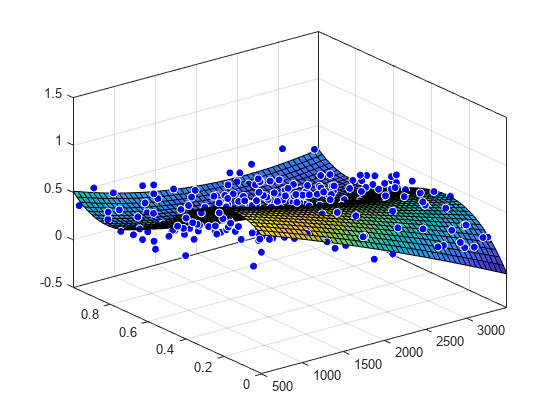
Figure contains an axes object. The axes object contains 2 objects of type surface, line. One or more of the lines displays its values using only markers

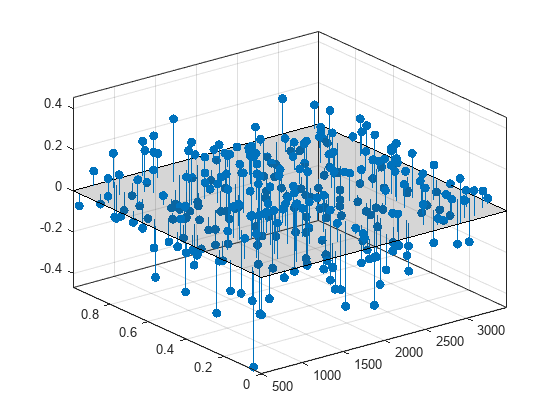
Plot the residuals fit.

plot(surffit,[x,y],z,'Style','Residuals')

Figure contains an axes object. The axes object contains 2 objects of type patch, stem.

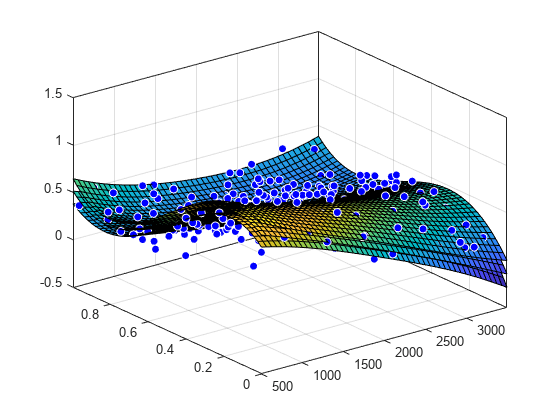
Plot prediction bounds on the fit.

plot(surffit,[x,y],z,'Style','predfunc')

Figure contains an axes object. The axes object contains 4 objects of type surface, line. One or more of the lines displays its values using only markers

Evaluate the Fit at a Specified Point

Evaluate the fit at a specific point by specifying a value for x and y , using this form: z = fittedmodel(x,y).

surffit(1000,0.5)
ans = 0.5673

Evaluate the Fit Values at Many Points

xi = [500;1000;1200];
yi = [0.7;0.6;0.5];
surffit(xi,yi)
ans = 3×1

    0.3771
    0.4064
    0.5331

Get prediction bounds on those values.

[ci, zi] = predint(surffit,[xi,yi])
ci = 3×2

    0.0713    0.6829
    0.1058    0.7069
    0.2333    0.8330


zi = 3×1

    0.3771
    0.4064
    0.5331

Get the Model Equation

Enter the fit name to display the model equation, fitted coefficients, and confidence bounds for the fitted coefficients.

surffit
     Linear model Poly23:
     surffit(x,y) = p00 + p10*x + p01*y + p20*x^2 + p11*x*y + p02*y^2 + p21*x^2*y 
                    + p12*x*y^2 + p03*y^3
       where x is normalized by mean 1982 and std 868.6
       and where y is normalized by mean 0.4972 and std 0.2897
     Coefficients (with 95% confidence bounds):
       p00 =      0.4253  (0.3928, 0.4578)
       p10 =      -0.106  (-0.1322, -0.07974)
       p01 =     -0.4299  (-0.4775, -0.3822)
       p20 =     0.02104  (0.001457, 0.04062)
       p11 =     0.07153  (0.05409, 0.08898)
       p02 =    -0.03084  (-0.05039, -0.01129)
       p21 =     0.02091  (0.001372, 0.04044)
       p12 =     -0.0321  (-0.05164, -0.01255)
       p03 =      0.1216  (0.09929, 0.1439)

To get only the model equation, use formula.

formula(surffit)
ans = 
'p00 + p10*x + p01*y + p20*x^2 + p11*x*y + p02*y^2 + p21*x^2*y + p12*x*y^2 + p03*y^3'

Get Coefficient Names and Values

Specify a coefficient by name.

p00 = surffit.p00
p00 = 0.4253

p03 = surffit.p03
p03 = 0.1216

Get all the coefficient names. Look at the fit equation (for example, f(x,y) = p00 + p10*x...) to see the model terms for each coefficient.

coeffnames(surffit)
ans = 9x1 cell
    {'p00'}
    {'p10'}
    {'p01'}
    {'p20'}
    {'p11'}
    {'p02'}
    {'p21'}
    {'p12'}
    {'p03'}

Get all the coefficient values.

coeffvalues(surffit)
ans = 1×9

    0.4253   -0.1060   -0.4299    0.0210    0.0715   -0.0308    0.0209   -0.0321    0.1216

Get Confidence Bounds on the Coefficients

Use confidence bounds on coefficients to help you evaluate and compare fits. The confidence bounds on the coefficients determine their accuracy. Bounds that are far apart indicate uncertainty. If the bounds cross zero for linear coefficients, this means you cannot be sure that these coefficients differ from zero. If some model terms have coefficients of zero, then they are not helping with the fit.

confint(surffit)
ans = 2×9

    0.3928   -0.1322   -0.4775    0.0015    0.0541   -0.0504    0.0014   -0.0516    0.0993
    0.4578   -0.0797   -0.3822    0.0406    0.0890   -0.0113    0.0404   -0.0126    0.1439

Find Methods

List every method that you can use with the fit.

methods(surffit)
Methods for class sfit:

argnames       category       coeffnames     coeffvalues    confint        dependnames    differentiate  feval          fitoptions     formula        indepnames     islinear       numargs        numcoeffs      plot           predint        probnames      probvalues     quad2d         setoptions     sfit           type

For more information on how to use a fit method, see sfit.

See Also

| | |